Руководство пользователя Matstat24
- Анатомия погрешности. Модель конверсии
- Как работает калькулятор погрешностей?
- Примеры использования калькулятора погрешностей
Анатомия погрешности. Модель конверсии
Введение
В учебниках по теории вероятности очень много умных академических слов. Но это руководство не классический учебник, а практическое руководство для директоров и маркетологов. Поэтому мы будем использовать устойчивые выражения: “покупки”, “заходы”, “лиды”, “потенциальные покупатели”, “конверсии”. Самым важным для нас будет такое понятие как “конверсия”.
Существует два подхода к определению того, что такое конверсия:
- “Экспериментальный”: конверсия определяется по классической формуле “Cv = лиды/визиты” или “покупки / потенциальные покупатели”. Этот подход позволяет нам определить точное значение конверсии, но при этом используются только известные данные из прошлого. При этом как правило мы получаем различные значения конверсии за соседние периоды времени даже когда все значимые параметры сайта и трафика остаются неизменными. Поэтому исходя из одной только “экспериментальной конверсии” мы часто не можем делать надежные прогнозы на будущее.
- “Теоретический”: конверсия определяется как “вероятность купить”, т.е. вероятность того, что посетитель сайта окажется целевым. Если бы мы смогли точно определить значение “теоретической конверсии”, это позволило бы нам легко делать достоверные выводы при сравнении двух конверсий, предсказывать показатели на следующий период. Поэтому встает задача эффективно оценить этот показатель.
Закон Больших Чисел гарантирует нам, что при растущем количестве испытаний “экспериментальная конверсия” будет стремиться к “теоретической”.
Более того, при помощи инструментов математической статистики мы можем построить интервалы, в которые с заданной достоверностью будет попадать “теоретическая конверсия” при заданном количестве лидов и визитов.
Для того чтобы понять, как строятся эти интервалы, опишем подробнее теоретическую модель. Пусть “теоретическая конверсия” принимает значение p из интервала от 0 до 1. Тогда каждому визиту можно сопоставить бернуллиевскую случайную величину (подбрасывание несимметричной монеты), которая с вероятностью p принимает значение “1”, если визит оказался целевым, и с вероятностью 1-p принимает значение “0”, когда визит нецелевой. Тогда мы можем посчитать вероятность того, что при заданном значении p у нас будет ровно k лидов после n визитов (это будет полиномиальное распределение), и наоборот при заданных количестве лидов и визитов мы можем оценить вероятность того, что p принимает какое-либо значение.
Иллюстрация закона больших чисел
Приведём примеры графиков плотностей вероятности того, что p принимает конкретное значение из интервала от 0 до 1 при фиксированных k и n (площадь под графиком означает вероятность попадания в заданный интервал):
1) При k=3, n=10
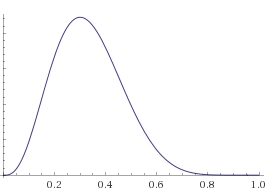
Т.е. при таких данных теоретическая конверсия с относительно большой вероятностью может принимать любое значение от 0,1=10% до 0,6=60%, т.е. мы не можем делать достоверных выводов по таким данным.
2) При k=15, n=50
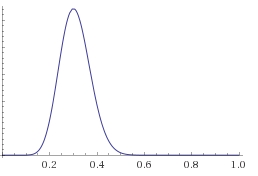
Мы видим, что график стал значительно более “узким”, вероятность попасть вне интервала от 0,15=15% до 0,5=50% пренебрежимо мала. Тем не менее, доверительный интервал для “теоретической конверсии” всё ещё очень широкий.
3) При k=450, n=1500
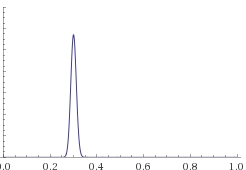
Видим, что при возрастающем числе конверсий “горбик” на графике становится всё более узким (при этом становится и более высоким). Тут мы можем утверждать, что с вероятностью более 99% теоретическая конверсия будет принимать значения от 25% до 35%.
Однако 100%-ый доверительный всегда равен всему отрезку от 0 до 1 (при подбрасывании монеты случайно можно получить подряд 1000 орлов, но очень-очень редко). Поэтому для того, чтобы делать выводы часто ограничиваются более слабыми условиями. Например, в медицинских исследованиях обычно ориентируются на доверительные интервалы, в которые исследуемая величина попадает с вероятностью 95%. В большинстве бизнес задач мы обычно ограничиваемся доверительными интервалами, в которые величина попадает с вероятностью 90-95%.
Например, при k=450, n=1500 теоретическая конверсия будет с вероятностью 90% попадать в интервал от (30 - 1,9)% = 28,1% до (30 + 1,9)% = 31,9%. Для краткости мы записываем это как 30% ± 1,9%, а величину 1,9% называет погрешностью конверсии.
Как работает калькулятор погрешностей?
Для того чтобы посчитать шансы, нужно внести в калькулятор данные нескольких экспериментов и нажать кнопку “Посчитать выбранные”.
Поле “Название” не обязательно для заполнения, по умолчанию пустая строка.
В поля “Визиты” и “Лиды” вводятся исходные данные. “Считаем с точностью” задаёт параметр P, выбирается из вариантов “66%, 75%, 80%, 90%, 95%, 99%”.
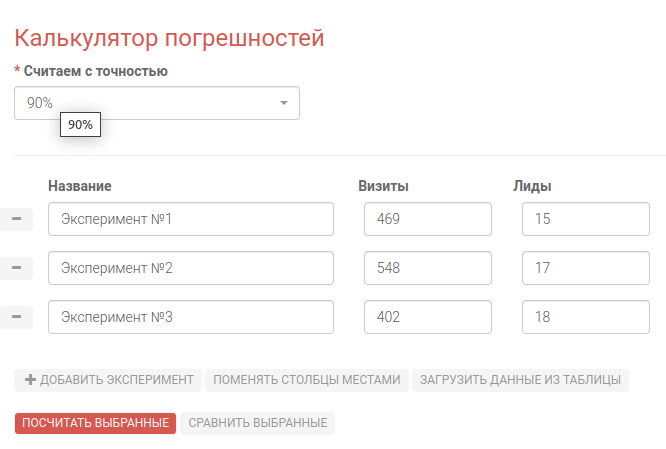
Опционально: возможность копировать Названия, Визиты и Лиды из электронных таблиц и вставлять в инструмент не по одному, а все разом.
В поле “Конверсия” в i-той строке выводится “Cv[i]±Eps[i]”. В шанс побить - B[i].
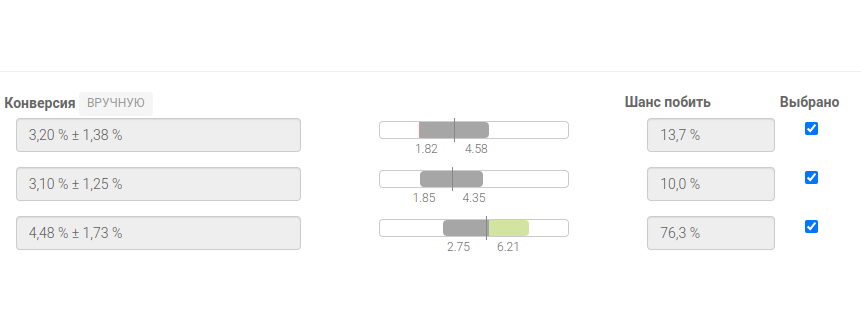
Если для одного из вариантов шанс побить больше 90%, то этот вариант выделятся зелёным цветом.
В доверительный интервал схематично рисуется интервал (Cv[i]-Eps[i],Cv[i]+Eps[i]) и его зоны пересечения с другими доверительными интервалами. Отображается не весь отрезок [0,1], а только его часть, содержащую полученные доверительные интервалы.
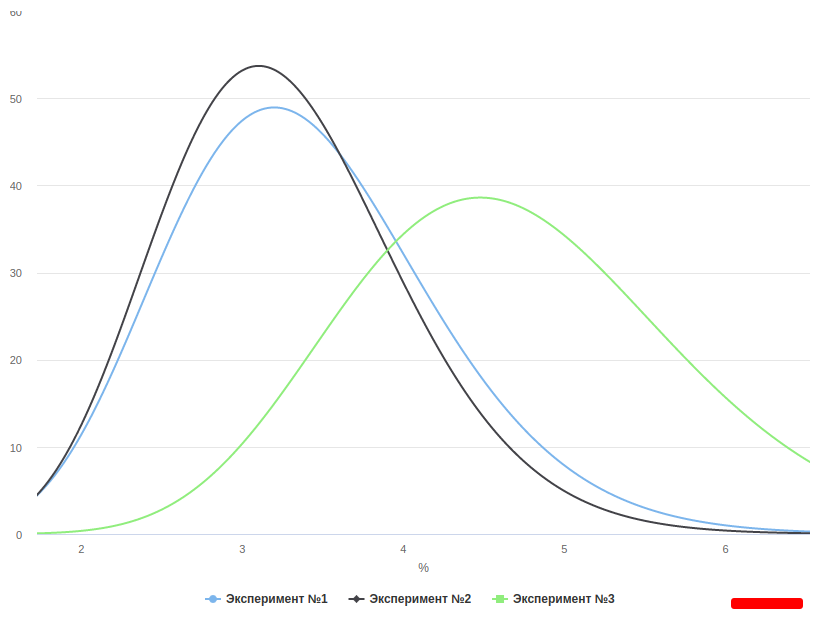
В поле “График” на одной картинке разными цветами строятся графики f[i]. Каждый график рисуется разным цветом и легендируется снизу. Картинку можно скопировать-вставить. Графики строятся в правильном масштабе. Пример графика:
Есть возможность добавить строку для ввода (плюсик) и удалить строку (крестик).
Справка:
Инструмент считает погрешность для конверсии и вероятность одного варианта оказаться лучше всех остальных.
Параметр Считаем с точностью означает вероятность, с которой конверсия попадает в полученный доверительный интервал. Чем больше точность, тем шире интервал.
Конверсия вычисляется как “(Лиды/Визиты)*100%”.
Вычисляется абсолютная погрешность, т.е. погрешность 5%±2% соответствует доверительному интервалу [(5-2)%;(5+2)%] = [3%;7%].
Шанс побить отображает вероятность одного варианта оказаться лучше всех остальных.
Познакомившись кратко с теорией и инструментам, перейдем к разбору практических задач.
Примеры использования калькулятора погрешностей
Как определить что очередное колебание лежит в пределах нормы?
При абсолютно одинаковых настройках рекламных кампаний, одинаковой сезонности, показатели всё равно колеблются из месяца в месяц. Как определить, очередное колебание лежит в пределах нормы или нет? Рассмотрим на примере.
Предположим, что на проекте за 3-ий месяц было 11358 визитов и 208 конверсий. Какой будет конверсия на следующий месяц, при условии отсутствия существенных доработок и скачков сезонности? Мы можем определить это при помощи мат.статистики, воспользовавшись калькулятором.

Это означает, что конверсия в следующем месяце с заданной вероятностью (по умолчанию 90%) примет значение в пределах от (1,83-0,20)% до (1,83+0,20)%. Значение 0,20% мы назовём погрешностью.
Другими словами, с вероятностью 90% конверсия за 4-ый месяц попадет в интервал от 1,63% до 2,03%. Этот интервал чисел называется доверительным интервалом.
Чем больше визитов, тем ýже будет доверительный интервал. Поэтому зачастую для предсказания конверсии используется статистика за несколько последних месяцев. Однако с этим нужно проявлять осторожность, потому что за это время может измениться сезонность, конъюнктура рынка или другие параметры, влияющие на конверсию.
И вот, собрав статистику по проекту за 4-ый месяц, мы получаем следующие показатели: 12792 визита, 219 конверсий и показатель конверсии 1,71%. Мы видим, что за месяц конверсия упала, но осталась в пределах доверительного интервала. Поэтому падение можно объяснить случайными факторами и ничего катастрофического не случилось.

В начале 5-го месяца, мы внедрили доработку, по итогам месяца получили 13525 визитов и 285 конверсий и хотим понять, увеличилась ли конверсия по сравнению с предыдущим периодом. Для этого можно воспользоваться другим инструментом математической статистики - шансом побить. Мы считаем, что один вариант лучше всех остальных, если шанс побить у него больше 90%. Воспользуемся калькулятором:

Мы видим, что шанс побить для 5-го месяца равен 93,0%. Это означает, что с вероятностью 93,0% сайт с доработками будет показывать более высокую конверсию, чем сайт без доработок. Поэтому гипотеза о том, что доработки повысили конверсию, подтвердилась.
Выбор лучшего и худшего исполнителя
В качестве примера возьмём отдел продаж, в котором работают 10 телемаркетологов.
Телемаркетологи обзванивают потенциальных клиентов и те клиенты, которые соглашаются на презентацию переводят на специалистов по продажам.
Руководителю такого отдела часто приходится решать задачи такого плана:
- какой план по заявкам поставить на сотрудников;
- нормально ли работает отдел;
- кто работает хорошо;
- кто работает плохо;
- стоит ли увольнять того кто работает хуже всех.
Пример №1
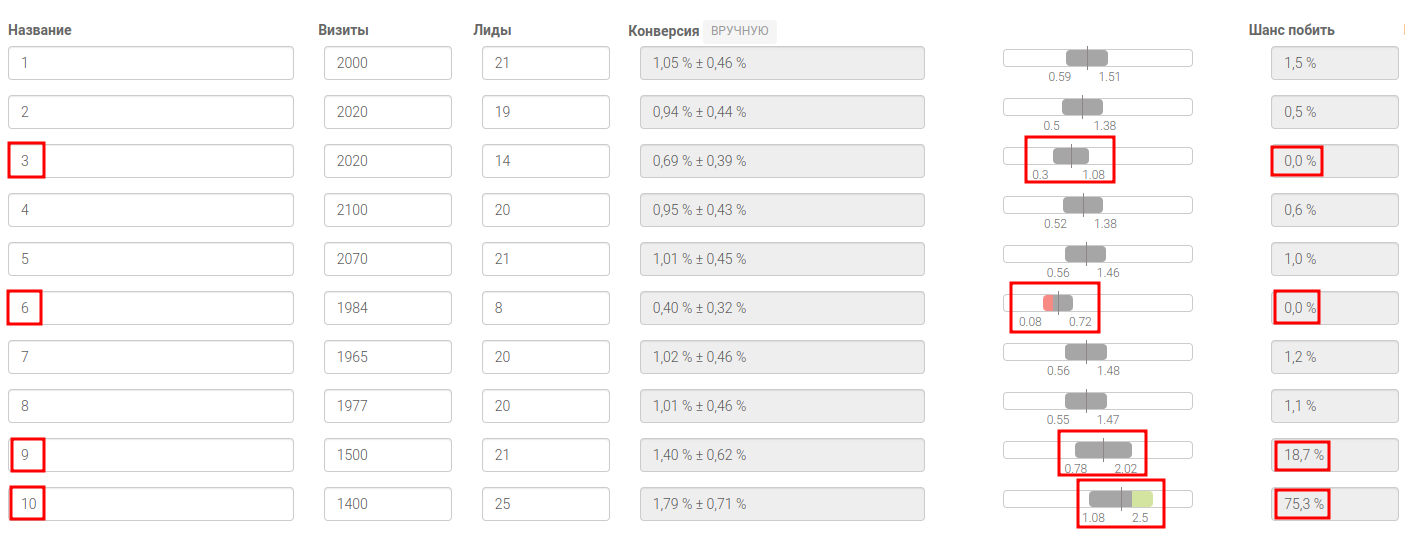
В примере №1 мы отразили основные параметры каждого сотрудника в отделе. Теперь на основе анализа данных ответим на все вышеперечисленные вопросы.
Какой план по заявкам устанавливать?
Посмотрим на доверительные интервалы сотрудников и проведем условные красные линии таким образом, чтобы красный и зеленые диапазоны были слева и справа от левой и правой красными линиями.
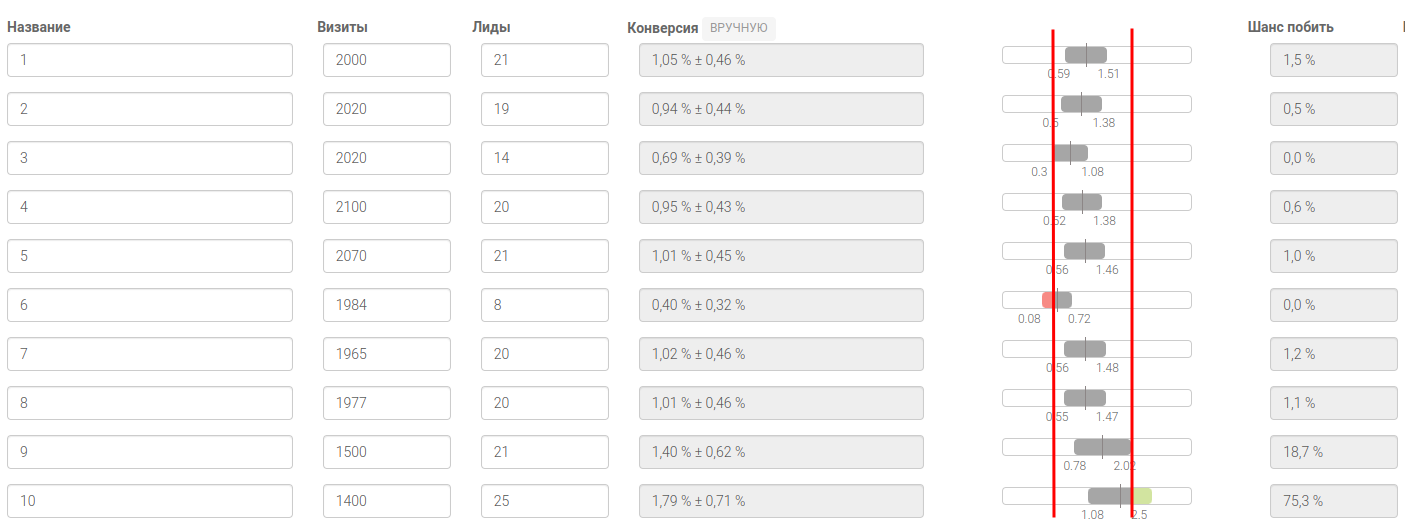
Мы можем увидеть, что у 8 из 10 сотрудников “пятна” доверительных интервалов “плавают” примерно посередине между красными линиями, следовательно план по заявкам корректировать не нужно. Если бы была ситуация когда большинство “пятен” были бы прижаты к правой или левой границе, то план по заявкам нужно было бы корректировать.
Нормально ли работает отдел?
Да, отдел работает нормально. Можно посмотреть на значения конверсий и убедиться в том, что большинство сотрудников имеют минимальные отклонения по показателю конверсия.
Кто работает хорошо?
Если посмотреть на показатель “Шанс побить”, то мы увидим, что сотрудники под номерами 9 и 10 имеют высокие показатели.
Кто работает плохо?
Ищем тех сотрудников у кого околонулевые показатели в колонке “Шанс побить”. Сотрудники под номерами 3 и 6 работают плохо.
Стоит ли увольнять того кто работает хуже всех?
В нашем примере кандидат на увольнение находится под номером 6, так как его конверсия вышла за пределы доверительного интервала большинства сотрудников. Что касается сотрудника под номером 3, то его увольнять пока не стоит, потому что он не попадает в красную зону. Статистика утверждает, что все сотрудники не могут выдавать результаты выше среднего, - это аксиома. Имеет смысл менять одного сотрудника на другого если есть шанс, что новый сотрудник будет выдавать результаты близкие к среднему в отделе.
Оценка итогов A/B тестирования
Для того чтобы получить приемлемые результаты A/B тестирования, нужно ориентироваться на показатель погрешности результата. Для экспресс-оценки выбирайте точность 95% и уровень погрешности менее 5%.
Пример №1
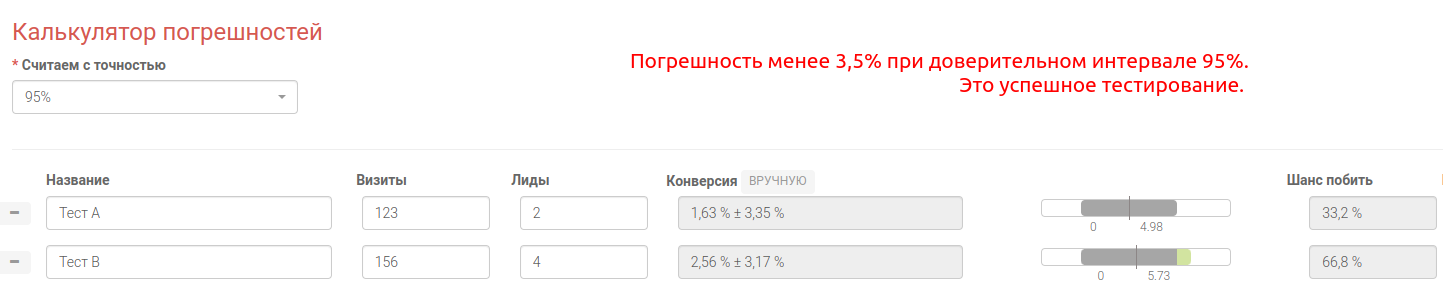
В примере №1 мы видим успешный A/B тест:
- погрешность менее 3,5%,
- конверсия в случае B отличается значительно в 1,57 раза,
- шансы побить примерно 2 к 1
Пример №2
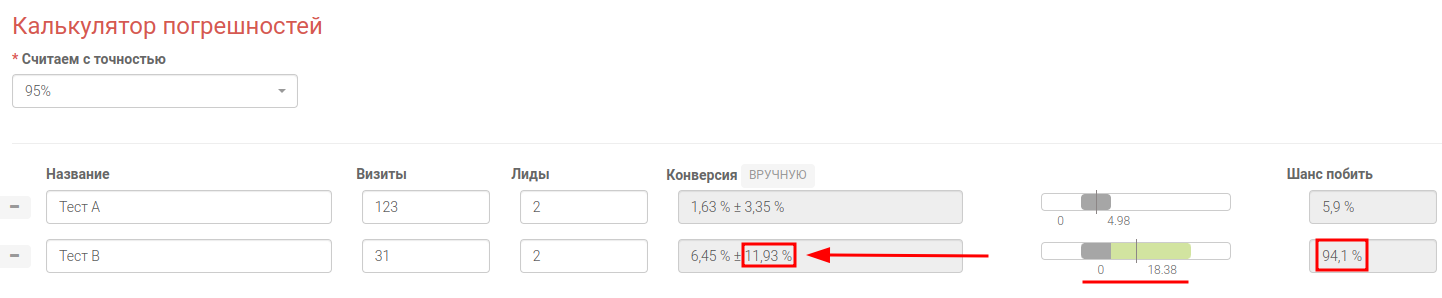
Во втором примере “Тест B” очень хороший показатель конверсии 6,45% против 1,63%, но на основе этих цифр нельзя принимать решение, потому что погрешность 11,93% выше чем 5%. Следовательно нужно продолжать проводить тест B, до тех пор, пока погрешность результатов не опустится до уровня <5%. Можно легко прикинуть какие должны быть параметры теста при сохранении текущей конверсии методом подбора.
Пример №2.1
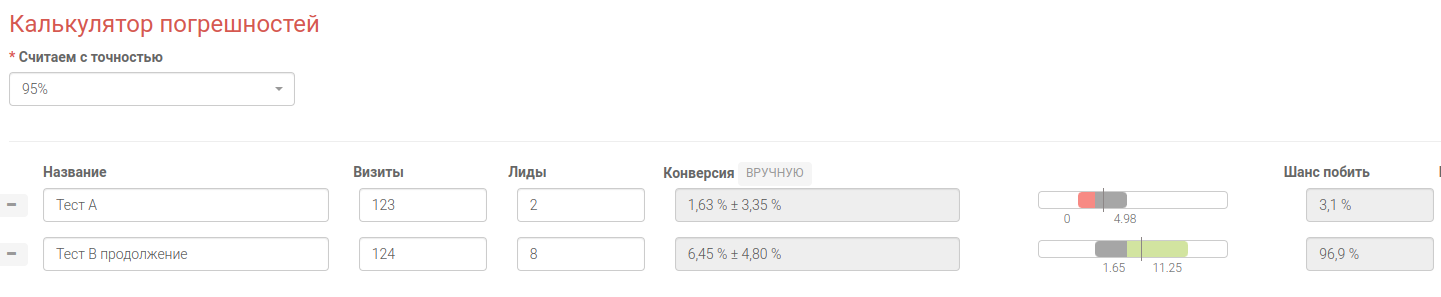
С помощью метода перебора, как мы видим при 124 визитах и конверсии 6,45% мы смогли уменьшить величину погрешности до уровня 4,8%. Следовательно вам нужно провести дополнительные 124 - 31 = 93 эксперимента в Тесте B, чтобы можно было принять достоверное решение.
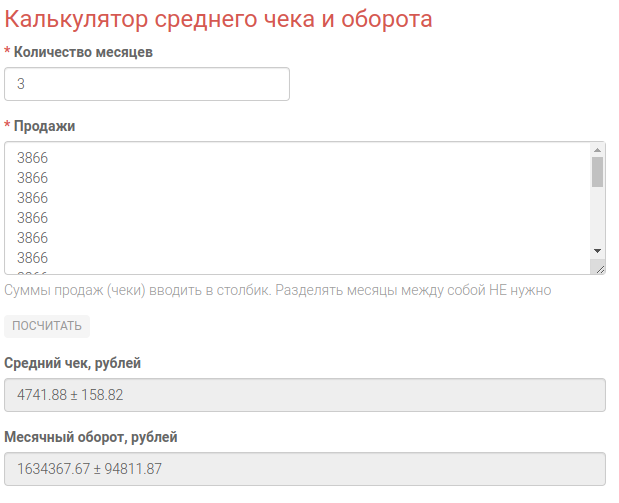
Предсказание среднего чека и оборота
Калькулятор считает средний чек, средний оборот и доверительные интервалы для уровня значимости 90%.
Если компания занимается продажей разных категорий товаров с принципиально разными средними чеками (например опт и розница), то нужно оценивать средний чек и оборот отдельно для каждой категории.
Данные следует собирать за месяцы, в которых не было аномального роста или падения продаж.